Rappel
Calculez l’angle formé par OX et la direction de coefficient angulaire 3. Si les axes forment un angle de 60° ?
Rappel
m = 3 tgɤ=3sin60°1+3cos60°=3√321+12=3√232=3√32.23=3√32
Motivation
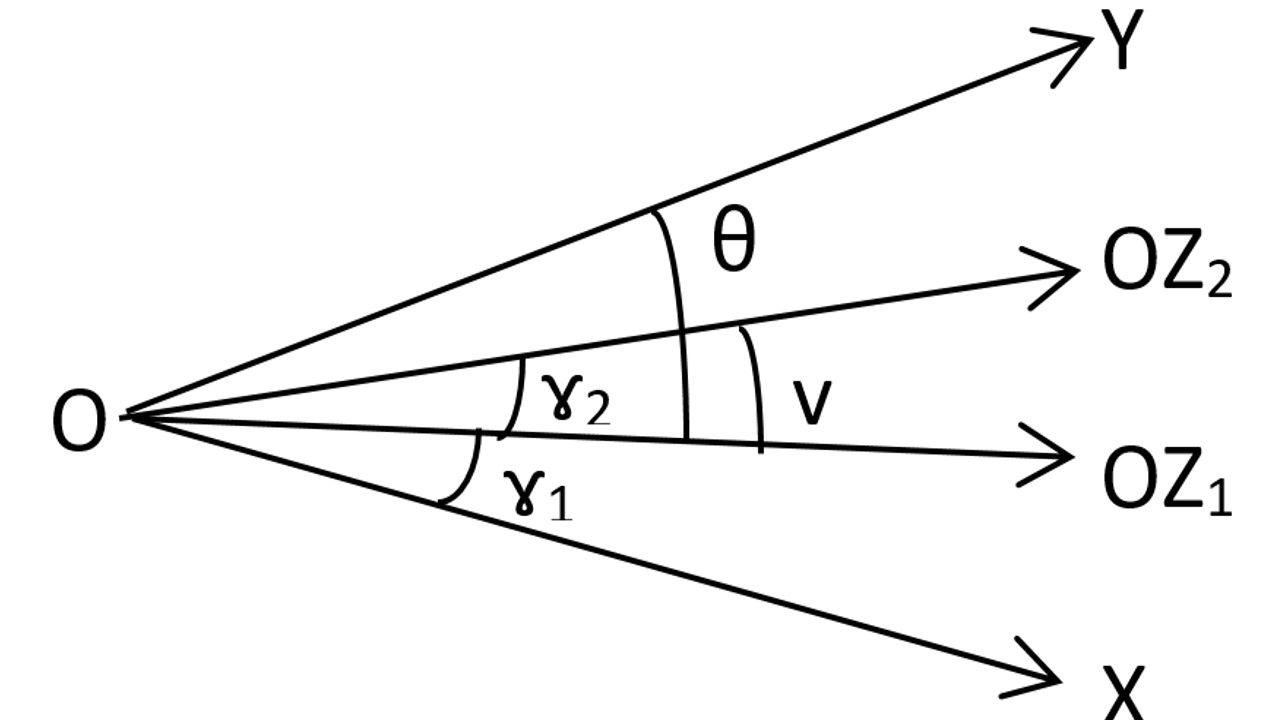
Que représentent OZ2 et OZ1 ?
Motivation
OZ1 et OZ2 sont les deux directions des angles ɤ 1 et ɤ 2.
Annonce du sujet
Qu’allons-nous étudier aujourd’hui en math ?
Annonce du sujet
Aujourd’hui nous allons étudier les angles de deux directions.
Que représentent V, ɤ 1 et ɤ 2 ?
Angle de deux directions
V = ɤ 2-ɤ 1 est l’angle formé par les deux directions,
ɤ 1 = l’angle formé par la direction OZ1 et l’axe OX.
ɤ 2 = l’angle formé par la direction OZ2 et l’axe OX.
Trouvons V ; on soit que tg (a-b) = tga−tb1+tgatgb
Comme V = ɤ 2-ɤ 1, on a
tg V = tg (ɤ 2-ɤ 1)
=\frac{tgɤ_2-tgɤ_1}{1+tgɤ_2 tgɤ_1} or \\ tgɤ=\frac{msinθ}{1+mcosθ}\\ =\frac{\frac{m_2 sinθ}{1+m_2 sinθ}-\frac{m_1 sinθ}{1+m_1 cosθ}}{1+(\frac{m_2 sinθ}{1+m_2 cosθ})(\frac{m_1 sinθ}{1+m_1 cosθ})}
Après transformation, on a :
| tg V =\frac{(m_2-m_1 )sinθ}{1+m_2 m_1+(m_2+m_1 )cosθ} |
Si θ = π/2
| tg V=\frac{m_2-m_1}{1+m_2 m_1} |
Calculez l’angle formé par la direction de coefficients angulaires respectifs \frac{4}{5} et -1/5.
Si θ = 60°
tg V=\frac{(-\frac{1}{2}-\frac{4}{5})sin60°}{1+(\frac{1}{5}.\frac{4}{5})+(-\frac{1}{5}+\frac{4}{5})cos60°}\\
=\frac{\frac{-\sqrt[]{3}}{2}}{1-\frac{4}{2}+\frac{3}{5}.\frac{1}{2}}=\frac{\frac{-\sqrt[]{3}}{2}}{1-\frac{4}{25}+\frac{3}{10}}\\
=\frac{\frac{-sqrt[]{3}}{2}}{\frac{50-8+15}{20}}=\frac{-sqrt[]{3}}{2}.\frac{47}{50}=\frac{-47\sqrt[]{3}}{100}
Calculez l’angle formé par la direction de coefficients angulaires respectifs \frac{4}{5} et -1/5.
Si θ = 90°
tg V=\frac{\frac{-1}{5}-\frac{4}{5}}{1+(\frac{-1}{5}-\frac{4}{5})}=\frac{-1}{1-\frac{4}{5}}=\frac{-1}{\frac{1}{5}}=1.\frac{5}{1}=-5
